初中数学作为中学教育的核心学科,初一阶段的知识体系构建直接影响后续学习的深度和广度。从数与代数的抽象思维到几何图形的空间想象,从方程的建模求解到概率统计的实际应用,初一数学为青少年打开了理性认知世界的大门。本文将从知识模块、核心概念、解题方法三个维度,系统梳理初一数学的完整知识框架,并通过表格形式总结关键公式和法则,助力学生建立结构化学习路径。
一、数与代数基础
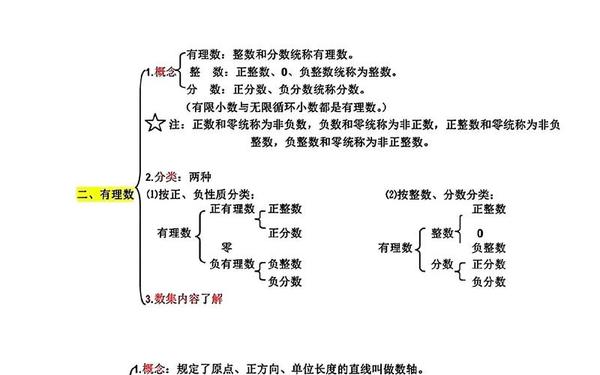
有理数是初中代数的核心概念,包含正数、负数和零的完整数系。其运算规则中,绝对值处理与符号判断是关键:例如异号相加时取绝对值较大数的符号,并用大绝对值减小绝对值。乘除运算遵循“同号得正,异号得负”的符号法则,科学记数法(a×10ⁿ)则要求1≤|a|<10,这在处理天体距离等大数据时尤为重要。
| 运算类型 | 规则要点 |
|---|---|
| 加法 | 同号相加符号不变,异号相减取大符 |
| 乘法 | 同号得正,异号得负,绝对值相乘 |
| 除法 | 除以非零数等于乘倒数,符号同乘法 |
整式运算体现代数思维的进阶,单项式的系数识别(如3x²的系数是3)与多项式次数判定(最高次项的次数)需特别注意。合并同类项时,字母部分完全相同的项才能系数相加,如2ab与-5ab可合并,而3a²b则不能。
二、几何初步认知
平面几何从点线面体展开,线段公理“两点之间线段最短”是解决最短路径问题的理论基础。角度的计算需注意单位换算(1°=60′,1′=60″),而余角、补角的性质在直角三角形证明中广泛应用。
平行线的判定与性质构成几何推理的双向逻辑:同位角相等则平行(判定),反之平行则同位角相等(性质)。这种互逆关系在解决折叠角、三角板组合等问题时尤为重要。平移变换保持图形全等且对应线段平行,其坐标规律(横纵坐标加减常数)是函数图像变换的基础。
| 图形类型 | 核心性质 |
|---|---|
| 线段 | 两点间最短路径,中点分线段等长 |
| 平行线 | 同位角相等,内错角相等,同旁内角互补 |
| 三角形 | 内角和180°,外角等于非邻内角和 |
三、方程与函数雏形
一元一次方程的解法遵循去分母、去括号、移项、合并、系数化为1的五步法则。移项变号规则(如+3移到右边变-3)是避免计算错误的关键。工程问题(工作量=效率×时间)和行程问题(路程=速度×时间)的建模训练,为后续函数应用打下基础。
函数概念虽在初一未完全展开,但正比例关系(如y=kx)的认知至关重要。数轴上的点与实数一一对应,为直角坐标系的学习埋下伏笔。统计图表(条形图、折线图)的解读能力,直接影响数据分析题的得分率。
四、概率统计启蒙
概率计算从古典概型入手,等可能性原则(如骰子各面概率均等)是基础。通过树状图或表格穷举所有可能结果,再计算特定事件概率(如点数和为7的概率)是典型解题路径。
有效数字的概念(从第一个非零数字起至末尾)在科学测量中广泛应用,如3.20×10³有三位有效数字。扇形统计图的圆心角计算(=比例×360°)需结合百分比理解。
| 概念 | 定义要点 |
|---|---|
| 必然事件 | 概率为1,如太阳 |
| 不可能事件 | 概率为0,如掷骰得7 |
| 随机事件 | 0<P(A)<1,如抛正面 |
总结与建议
初一数学知识体系呈现“基础性”与“过渡性”双重特征,既包含算术到代数的思维跃迁,又孕育着几何证明与函数思想的萌芽。建议学习者:1)通过思维导图构建知识网络,例如将有理数运算规则与整式法则对比记忆;2)在几何证明中强化因果逻辑链书写,避免跳步;3)通过跨学科项目(如计算家庭水电费的函数关系)深化数学应用认知。未来研究可探索AR技术辅助几何空间想象、游戏化概率实验等新型学习模式,使数学认知更贴合数字原生代的学习特征。