数学作为基础学科的核心,其知识体系的构建需要从小学阶段开始逐步积累与深化。四年级上册的内容既是对低年级知识的延伸,又是为高年级抽象思维训练奠定基础的关键环节,而1至6年级数学公式的系统性掌握则是解决复杂问题的核心工具。本文将通过结构化梳理和典型案例分析,探讨如何高效掌握四年级核心知识点与全学段公式规律。
知识体系与核心概念
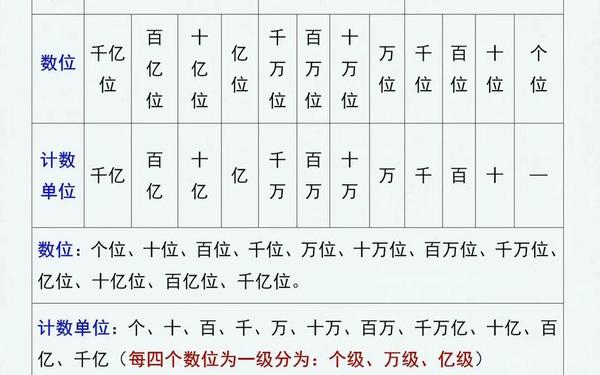
四年级上册数学以大数的认识为起点,通过十进制计数法理解“十万”“亿”等数量级,强调数位与计数单位的区别,例如“千位是位置,千是单位”。在几何领域,公顷与平方千米的换算要求学生掌握面积单位间的进率关系,如1平方千米=100公顷=1,000,000平方米,并通过实例(如香港面积约1100平方千米)建立量感。
角的度量单元突破传统图形认知,通过量角器操作与角度分类(锐角、直角、钝角、平角、周角),培养学生空间观念。例如,平角由射线旋转半周形成,1周角=2平角=4直角的关系需通过动态演示强化理解。三位数乘两位数的笔算方法要求对齐数位并分步叠加,这一算法为后续小数乘法奠定基础。
公式规律与应用场景
小学阶段公式可分为运算规律、几何计算与应用模型三类。运算定律中,乘法分配律(a±b)c=ac±bc贯穿四到六年级,例如计算125×88时拆分为125×(80+8)=10,000+1,000=11,000,显著提升效率。几何公式的层级递进体现在从长方形面积(长×宽)到长方体体积(长×宽×高)的扩展,而圆的周长公式C=πd则需结合π的近似值3.14进行实际计算。
应用类公式如单价×数量=总价和速度×时间=路程,需通过生活案例训练建模能力。例如“汽车3小时行驶240千米”可推导速度=80千米/时,并延伸至相遇问题(速度和×时间=总路程)。以下表格对比典型公式及其认知层级:
| 公式类型 | 四年级重点 | 全学段延伸 |
|---|---|---|
| 运算律 | 乘法分配律 | 分数四则运算 |
| 几何计算 | 公顷换算 | 圆柱侧面积=2πrh |
| 应用模型 | 路程问题 | 追及问题(速度差×时间) |
学习策略与认知工具
构建知识结构图是梳理零散知识点的有效方法。例如将“大数的认识”分解为读写规则、比较方法、近似值计算三大模块,并与后续小数知识形成连接。研究表明,使用思维导图的学生在单元测试中正确率提高约18%。
在公式记忆方面,错题归纳法与多维练习法相结合效果显著。例如针对乘法分配律的常见错误(如漏乘括号外项),可通过专项错题本记录并设计变式题强化记忆。计算器的合理使用(如ON/C与AC键功能区分)亦能提升大数计算的效率。
总结与建议
四年级上册数学的知识点与公式体系呈现明显的螺旋上升特征,例如从整数运算到分数概念的引入,从平面图形到立体几何的拓展。教师需注重知识迁移能力的培养,例如将“四舍五入法”从大数近似值延伸到小数保留位数。未来研究可进一步探索基于AI的个性化公式训练系统,通过分析学生错题数据动态调整学习路径。
建议家长在辅导过程中采用“问题链”引导法,例如在购物场景中串联单价计算、货币换算与折扣问题,使公式应用融入真实情境。教育者亦可借鉴新加坡数学的CPA(具象-形象-抽象)教学模型,通过实物操作深化公式理解。

